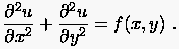
In diesem Kapitel befassen wir uns mit der Aufgabe, die linearen Gleichungssysteme, welche man aus der diskretisierten Differentialgleichung erhält, unter Berücksichtigung ihrer speziellen Struktur möglichst effizient zu lösen. Diese Gleichungssysteme haben besondere Eigenschaften: Die Koeffizientenmatrizen sind meist sehr groß, aber einfach strukturiert. Sie sind `schwach besetzt', die von Null verschiedenen Elemente treten in regelmäßiger `bandartiger' Weise in bestimmten charakteristischen Größenverhältnissen auf. Um einen ersten Eindruck zu vermitteln, wollen wir im folgenden zunächst den Prototyp einer elliptischen Differentialgleichung 2. Ordnung, die sogenannte Poissongleichung betrachten.
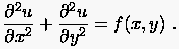 |
(5.1) |
Der Einfachheit halber beschränken wir uns auf ein quadratisches Integrationsgebiet und Dirichletsche Randbedingungen. Gesucht ist die Lösung , welche im Gebiet die PDG erfüllt und auf dem Gebietsrand die vorgegebenen Werte
annimmt. Zur Diskretisierung der Randwertaufgabe legen wir ein quadratisches Rechengitter der Schrittweite zugrunde. Die Anzahl der Unbekannten verhält sich dann wie ,
was bei einer Unterteilung von
,
was bei einer Unterteilung von  ca.
Unbekannte ergibt. Die Gestalt der
Koeffizienten-Matrix hängt von dem gewählten
Differenzenquotienten für
ca.
Unbekannte ergibt. Die Gestalt der
Koeffizienten-Matrix hängt von dem gewählten
Differenzenquotienten für 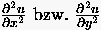 ab. Wählt man zur
Approximation der zweiten partiellen Ableitung jeweils den
zentralen Differenzenquotienten (2.12), so ergibt sich
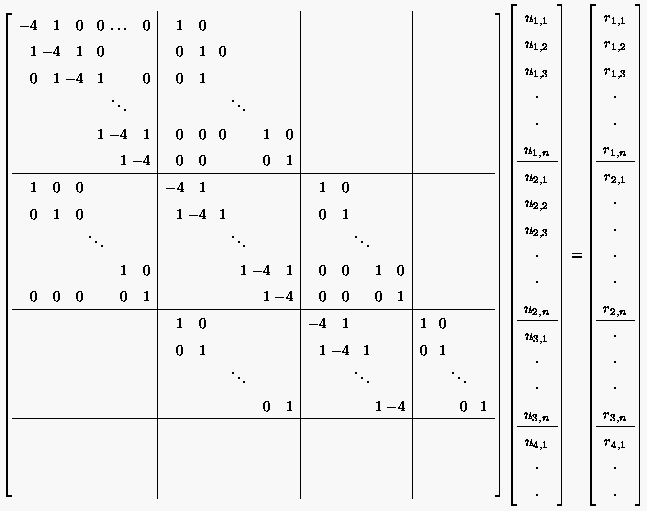
das folgende Gleichungssystem
ab. Wählt man zur
Approximation der zweiten partiellen Ableitung jeweils den
zentralen Differenzenquotienten (2.12), so ergibt sich
das folgende Gleichungssystem
| (5.2) |
oder mit auf der rechten Seite das System, das im folgenden abgedruckt ist.
Auf dieses Gleichungssystem läßt sich jedes Verfahren zur Lösung linearer Probleme anwenden. Die Effizienzunterschiede sind jedoch beträchtlich. So führt z.B. die Cramersche Regel auf ein Jahre währendes Geduldspiel, wohingegen moderne Verfahren bereits nach ca. 8 Sekunden zu einer Lösung gelangen. Entscheidend für die Effizienz eines Verfahrens ist der zu bewältigende Rechenaufwand, also die Anzahl der arithmetischen Operationen zur Bestimmung der Lösung. Einen ersten vergleichenden Überblick kann man sich anhand der Tabelle 7 verschaffen, die sich auf das oben skizzierte Problem bezieht.
Grundsätzlich wird zwischen direkten Lösungsmethoden, welche auf der sukzessiven Elimination der Unbekannten basieren, und iterativen Prozessen, die die gesuchte Lösung als Folge von Näherungen bestimmen, unterschieden. Der bekannteste Vertreter, der hier nicht näher diskutierten direkten Methode, ist das herkömmliche Gaußsche Eliminationsverfahren. Daneben seien das Cholesky-Verfahren zur Dreieckszerlegung symmetrisch positiver Bandmatrizen, der Thomas-Algorithmus usw. in Erinnerung gerufen.
Die direkten
Lösungsmethoden erfordern die Speicherung der gesamten
Koeffizientenmatrix, wodurch es leicht zur Erschöpfung des zur
Verfügung stehenden Arbeitsspeichervolumens kommen kann. Die
Rechenzeit wird in der Folge zu einem nicht unerheblichen Teil für die
Datenkommunikation mit Hilfsspeichermedien verbraucht, weshalb sich
die Lösung vor allem bei niedriger Übertragungsgeschwindigkeit
erheblich verzögern kann. Mittlerweile existieren jedoch
Algorithmen, die solchen Nachteilen durch sukzessive Zusammensetzung
der linearen Gleichungssysteme in Verbindung mit gleichzeitiger
Elimination begegnen (sog. Frontlösungsmethoden). Daneben
zeichnen sich die direkten Verfahren durch die unangenehme Eigenschaft
aus, die numerischen Störungen der exakten Lösung (z.B.
Rundungsfehler) zu akkumulieren. Den entscheidenden Parameter zur
Bestimmung der Empfindlichkeit gegenüber Störungen stellt die
Konditionszahl einer Matrix (also das Produkt 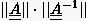 nach
beliebiger Norm) dar, für die man folgende `Faustregel' findet:
nach
beliebiger Norm) dar, für die man folgende `Faustregel' findet:
`Wird ein lineares GleichungssystemZur Senkung der Konditionszahl verfügt die Numerik über möglicherweise Abhilfe verschaffende Methoden, wie Equilibrieren, Pivotisieren, Vorkonditionieren, usw.mit -stelliger dezimaler Gleitkommarechnung gelöst, und beträgt die Konditionszahl der Koeffizientenmatrix , so sind aufgrund der im allgemeinen unvermeidlichen Eingangsfehler nur Dezimalstellen der auf die betragsmäßig größte Komponente bezogene Lösung sicher.'
Im allgemeinen sind direkte Methoden wirkungsvoller als iterative Methoden, sobald