Methode der Fourierreihen

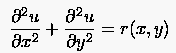
Zur effizienten Lösung der bei der Approximation zweidimensionaler elliptischer Probleme typischerweise auftretenden pentadiagonalen Gleichungssysteme (vgl. Gleichung (5.12)) kann alternativ die direkte Methode der Fourierreihen verwendet werden. Sie ist mathematisch mit einer Eigenwert-Eigenvektor-Transformation vergleichbar. Eine verständliche Herleitung des Verfahrens ist von Le Bail [21] angegeben. Das Prinzip der Methode der Fourierreihen wird im folgenden am Beispiel des numerischen Lösungswegs der Poisson-Gleichung

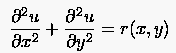(5.66)

mit Dirichlet-Randbedingungen für ein rechteckiges Gebiet verdeutlicht.

Die zentrale Differenzenapproximation der Poisson-Gleichung führt für jeden Punkt $P$_i,j auf die bekannte 5-Punkte-Differenzenformel:

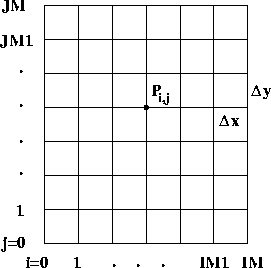
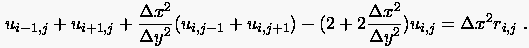(5.67)

Die Randbedingungen seien durch die entsprechenden Werte $u$_0,j, u_IM,j, u_i,0 sowie $u$_i,JM gegeben.

Da die Methode der Fourier-Reihen (Sinus-Reihen) als Randwerte immer den Wert Null benötigt, bestimmen wir nun eine neue Unbekannte $u$_i,j⁶⁸²⁶* mit $u$_i,j⁶⁸²⁷* = u_i,j für und $u$_i,j⁶⁸²⁹* = 0 für $i=0$ und $i=IM$. Es gilt für alle Zeilen :

Im folgenden wird $u$ anstatt $u*$ geschrieben.

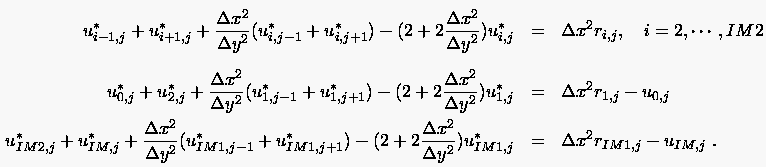
Die allgemeine Form von Differenzengleichungen, die sich mit Hilfe der Fourierreihenmethode behandeln lassen lautet:

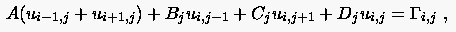(5.68)

und ist für ein konstantes $j$ eindeutig darstellbar durch die Fourier-Sinus-Reihe (Fourier-Synthese):

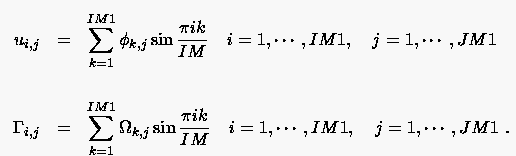(5.69)

Die erste Reihe beschreibt eine periodische Funktion mit den Randwerten $u$_0,i= u_IM,j=0. Die Fourier-Koeffizienten einer Sinus-Reihe sind nachfolgend angegeben (Fourier-Analyse):

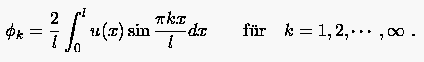(5.70)

Bei endlicher Anzahl von Funktionswerten $u(x)=u$_i,j für konstantes $j$ führt die Trapezregel auf:

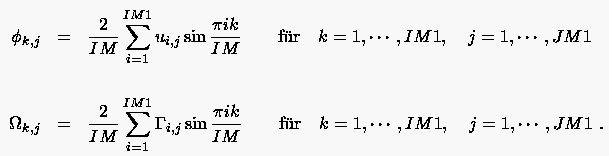(5.71)

Für $j=0$ und $JM$ ist $$_k,j mit bekannten Funktionswerten $u$_i,j nun bekannt.
Setzt man die Fourier-Sinus-Reihe für $u$_i,j und $$_i,j in die Differenzengleichung ein

so kann die eckige Klammer mit der trigonometrischen Summenformel

umgeschrieben werden:

Klammern wir in der Gleichung den Term $sin\{\pi ikIM\}$ aus, folgt:

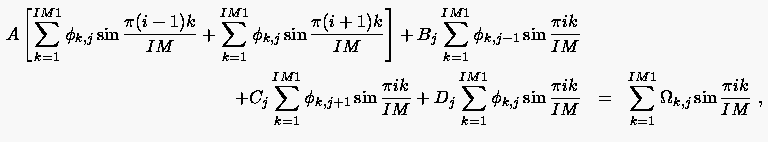
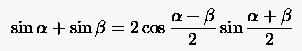
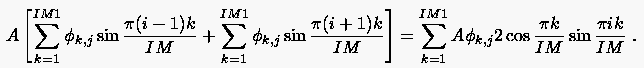
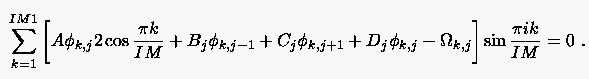(5.72)

Dieser Ausdruck ist identisch mit dem linearen System eindimensionaler Differenzengleichungen in $y$-Richtung zur Bestimmung der Fourier-Koeffizienten $$_k,j für jeweils konstantes $k$:

Es sind hier nun $IM1$ tridiagonale Gleichungssysteme mit jeweils $JM1$ Unbekannten zu lösen. Die Werte der gesuchten Funktion $u$_i,j an den Gitterpunkten werden dann durch Fourier-Synthese geliefert.

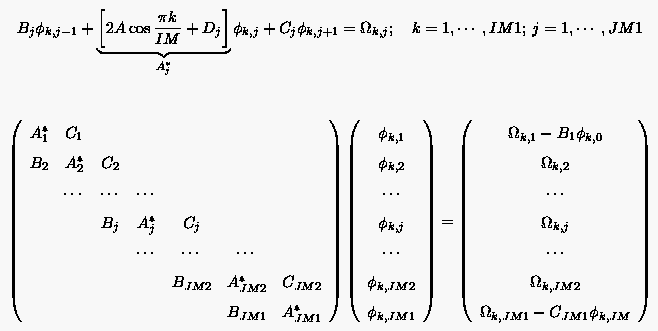
Die Methode der Fourier-Reihen setzt sich demnach für zweidimensionale Probleme aus drei Schritten zusammen:

1. Fourier-Analyse in $x$-Richtung.
   Die Nicht-Nullrandbedingung in $x$-Richtung muß vorher im $$_1,j,   _IM1,j
   eingearbeitet werden. $$_{i,j k,j}
2. Lösung $IM1$ tridiagonaler Gleichungssysteme
   mit jeweils $JM1$ Unbekannten in $y$-Richtung. $$_{k,j k,j}
3. Fourier-Synthese in $x$-Richtung. $$_k,j u_i,j

Der Vorteil der Methode besteht darin, daß das pentadiagonale Gleichungssystem (5.68) auf eindimensionale tridiagonale Systeme zurückgeführt werden kann, die rekursiv mit geringem Rechenaufwand lösbar sind. Dieser Vorgang wird auch als Faltung bezeichnet. Eine wesentliche Einschränkung des Verfahrens beruht auf dem Koeffizienten $A=konst$ in Gleichung (5.68). Der Einfluß des rechten und linken Nachbarn muß hier jeweils gleich sein.

Bei der elementaren Durchführung der Transformation (5.71) für die rechte Seite der Differenzengleichung (Fourier-Analyse) und Gleichung (5.69) zur Bestimmung der Lösung (Fourier-Synthese) werden für jede der $j$ Zeilen $M2$ Multiplikationen und ebensoviele Additionen benötigt. Die für die Brauchbarkeit des Verfahrens wesentliche Verbesserung war, daß sich die Anzahl der Operationen durch einen Algorithmus, der unter dem Namen Fast Fourier Transforms (FFT) bekannt wurde, entscheidend verringern läßt. FFT benötigt etwa $0.721\; x\; IM\; x\; ln(IM)$ Multiplikationen für konstantes $j$ und ist durchführbar für alle $IM=2n,\; n$Element von N.