Die Beziehung zwischen den Gittern wird durch Restriktions- und Interpolationsoperatoren hergestellt. Restriktionsoperatoren bilden Gitterfunktionen eines feinen Gitters auf solche eines gröberen Gitters ab, beispielsweise
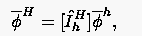
Wir wollen uns auf die übliche Gittersequenz beschränken. ist im allgemeinen Fall (Full weighting) ein Operator, der über sämtliche Nachbarn mittelt.
Diese Darstellung gilt natürlich nur für randferne Punkte. Ansonsten müssen die Gewichte der Nachbarwerte geeignet modifiziert werden. Prinzipiell sind auch anders gewichtete Restriktionsoperatoren möglich, häufig verwendet man lediglich die einfache Injektion. Hierbei wird einem Aufpunkt des groben Gitters der entsprechende Feingitterwert des physikalisch gleichen Punktes zugeordnet. Die Lösung der Grobgittergleichung muß relativ genau erfolgen, da sonst die errechneten Fehler keine sinnvolle Korrektur darstellen. Nach der Lösung erfolgt die Interpolation der Lösung auf ein feineres Gitter.
Der Restriktionsoperator für die Lösung und das Residuum wird wie folgt definiert:
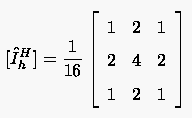
Interpolationsoperatoren bilden die Gitterfunktionen eines groben Gitters auf ein feines ab. Die Methode der lokalen Fourierreihenentwicklung zeigt, daß die Interpolationsvorschrift konsistent zur Ordnung des Diskretisierungsverfahrens sein sollte. Die Ursache hierfür liegt darin, daß durch die Interpolation von auf Interpolationsfehler erzeugt werden, die sich wiederum in Schwingungskomponenten zerlegen lassen. Bei Interpolation von zu geringer Ordnung erhält man möglicherweise neue niederfrequente Fehleranteile. Dieser Effekt kann die Effizienz des Verfahrens zerstören.
Der Prolongationsoperator wird für die Interpolation der
Feingitterkorrektur aus der Grobgitterkorrektur
benötigt. Hier kann die bilineare Interpolationsformel
benutzt werden:
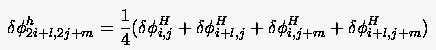 |
(5.94) |
mit und .