Iterative Anpassung der Kontrollfunktionen zur Einarbeitung von Randorthogonalität und Vorgabe der Maschenweite normal zur Wand

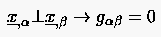
In der vorangegangenen Methode wurde die Verteilung der Kontrollfunktionen im gesamten Rechengebiet einzig und allein aus der Punkteverteilung auf den Randflächen bestimmt. Zwar konnten dadurch die Kontrollfunktionen auf einfache Weise direkt ermittelt werden, jedoch hat man keine Möglichkeit der Einflußnahme auf das Netz bezüglich Maschenweite und Orthogonalität auf dem Rand. Neben der Vorgabe der kartesischen Koordinaten der Randpunkte, die als Randbedingungen in das elliptische DGL.System 2. Ordnung in Gleichung (6.120) eingehen, können im allgemeinen durch die freie Wahl der drei Kontrollfunktionen $$ prinzipiell drei weitere Bedingungen in den Gittergenerierungsprozeß eingebracht werden. Betrachtet man dazu die Fläche $$ = const., in der die beiden Kurvenscharen $$ und $$ verlaufen, dann sollen diese drei Bedingungen formuliert werden als die beiden Orthogonalitätsforderungen

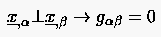(6.126)

(6.127)

sowie die Vorgabe der Maschenweite

(6.128)

auf der Wand entlang der Koordinatenlinie $$ .

Abbildung 85: Orthogonalitäts- und Maschenweitenvorgabe auf der Koordinatenfläche $$ = const.

Die entsprechende mathematische Formulierung kann unter Berücksichtigung von:

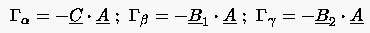(6.129)

auf der Koordinatenfläche $$ = const. geschrieben werden mit

Analoge Beziehungen für die Koordinatenflächen $$ bzw. $$ = const. ergeben sich durch zyklisches Vertauschen von $$, und $$ in der Gleichung (6.129). Alle hierin auftretenden Größen, außer $x$_, im Term $A$, lassen sich aus der Punkteverteilung auf der Randfläche und der vorgegebenen Maschenweite $g$ normal zur Fläche bestimmen. Die Ermittlung der Größe $x$_, erfolgt schließlich in dem folgenden iterativen Prozeß:

1.

Annahme der Kontrollfunktionen $$_i auf dem Rand

2.

Interpolation von $$_i vom Rand ins Gebietsinnere

3.

Bestimmung des Gitters durch Lösung der DGL. (6.120)

4.

Bestimmung von $x$_, auf dem Rand durch einseitige Differentiation
$$ Bestimmung der Kontrollfunktionen $$_i mit der Gleichung (6.129)

5.

Iteration von 2. bis 4. bis zur Konvergenz

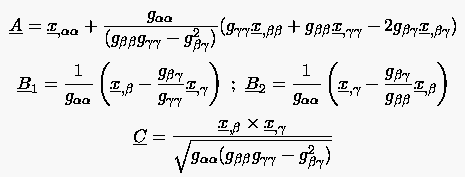
Eine mögliche Erweiterung dieser Methode besteht darin, die beschriebene Vorgehensweise auf mehrere aufeinanderfolgende Koordinatenflächen $$ =const. anzuwenden. Ausgehend von der ersten Maschenweite normal zur Wand werden die folgenden Maschenweiten zwischen benachbarten Punkten entlang der $$-Koordinatenlinien gemäß einer Sinushyperbolikus-Verteilung bestimmt. Darüber hinaus kann damit auch eine gewisse Eindringtiefe bezüglich der Orthogonalität bewirkt werden.