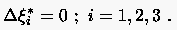
Zur Erklärung des theoretischen Hintergrunds ist es hilfreich, zunächst ein Basiskoordinatensystem einzuführen, dessen einzelne Komponenten der Laplacegleichung genügen:
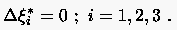 |
(6.116) |
Transformiert man weiterhin das System auf ein neues Koordinatensystem (das eigentlich zu generierende System) , dann folgt aus der Gleichung (6.116)
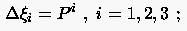 |
(6.117) |
mit
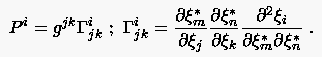 |
(6.118) |
In dieser Gleichung sind die kontravarianten Metrikkoeffizienten. Die sind durch die Transformation von nach bestimmt und stellen die Verzerrung des zu generierenden Gitterkoordinatensystems und des Basiskoordinatensystems dar.
Dies legt nahe, die Gleichung (6.117) als allgemeines Gittergenerierungssystem zugrundezulegen, wobei der Verzerrungsfaktor nicht über Gleichung (6.118), sondern als Kontrollfunktion direkt zu bestimmen ist.
Die Lösung der Gleichung (6.117) stellt die krummlinigen Koordinaten als Funktion der kartesischen Ortskoordinaten dar. Wünschenswert wäre aber, den umgekehrten funktionalen Zusammenhang, d.h. die Gitterpunkte im physikalischen Gebiet in Abhängigkeit der krummlinigen Koordinaten, zu kennen. Dazu wird die Gleichung mit multipliziert und es folgt:
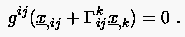 |
(6.119) |
Die krummlinigen Koordinaten bilden ein rechteckiges, äquidistantes Gitternetz in der ''computational domain'', in dem die berandenden Koordinatenlinien bzw. -flächen den physikalischen Randlinien bzw. -flächen entsprechen. Damit wird die Lösung von Gleichung (6.117), d.h. die Punkteverteilung in der ''physical domain'', durch die die Oberfläche beschreibenden kartesischen Koordinaten der Randpunkte bestimmt.
Die wichtigsten bzw. dominierendsten Kontrollfunktionen
sind 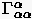 (
(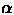 = 1, 2, 3),
die jeweils einer in jeder Koordinatenrichtung unabhängigen
Verzerrung entsprechen. Setzt man nun alle
anderen Kontrollfunktionen zu null, das heißt
= 1, 2, 3),
die jeweils einer in jeder Koordinatenrichtung unabhängigen
Verzerrung entsprechen. Setzt man nun alle
anderen Kontrollfunktionen zu null, das heißt
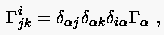
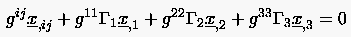 |
(6.120) |
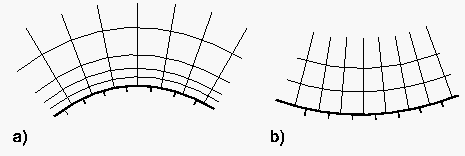
Wenn die Kontrollfunktionen null sind, dann reduziert sich Gleichung (6.120) auf die Laplace-Gleichung, die ein glattes Gitternetz erzeugt. Das auf diese Weise erzeugte Netz zeigt die Tendenz, Gitterlinien über konvexen Berandungen zu konzentrieren und über konkaven Rändern auseinanderzuziehen.
 |
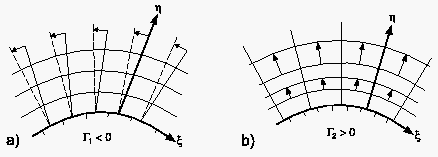
Nimmt man jedoch die Kontrollfunktionen in Gleichung (6.120) hinzu, dann bewirken negative Werte für eine Bewegung der Linien oder Flächen in Richtung anwachsender Werte; positive Werte haben den entsprechend entgegengesetzten Effekt. Diese Eigenschaft wird dazu benutzt, Gitterpunkte in gewissen Bereichen, z.B. an einer festen Wand, zu konzentrieren.
 |
Die Auswertung und Bestimmung der Kontrollfunktionen erfolgt in einem automatisierten Prozeß entweder anhand eines vorgegebenen algebraischen Netzes oder durch Interpolation der Randpunkteverteilung ins Gebietsinnere. Beide Methoden werden im folgenden beschrieben.