Kubische Splinefunktion

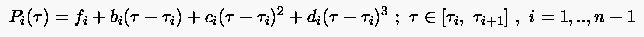
Betrachtet wird zunächst eine Funktion $f($) , die an den n Stützstellen $$_i ( i = 1 , ..., n ) durch die Stützwerte $f$_i = f (_i ) gegeben ist.

Der Funktionsverlauf innerhalb der einzelnen Intervalle wird durch Polynome 3. Grades interpoliert:

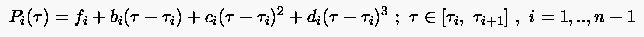(6.63)

Es wird verlangt, daß die Interpolationsfunktionen an der Intervallgrenze zweifach stetig differenzierbar sind:

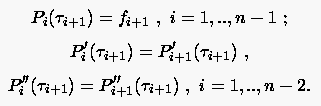(6.64)

Die Bestimmung der Polynomkoeffizienten erfolgt nach den Gleichungen für

$c$_i :

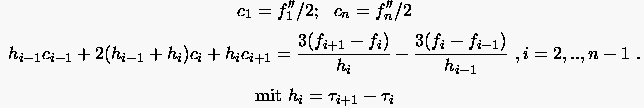(6.65)

$b$_i :

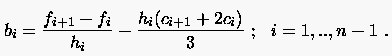(6.66)

$d$_i :

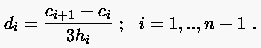(6.67)

Die Koeffizienten von Gleichung (6.65) bilden eine tridiagonale Matrix. Durch LU-Zerlegung oder Gauss-Elimination lassen sich die $c$_i effizient berechnen. Danach folgt die Auswertung von $b$_i, d_i nach den Formeln (6.66) und (6.67). Somit sind alle Koeffizienten des Interpolationssplines festgelegt.

Eine alternative Methode mittels Hermitescher Interpolation

Im letzten Abschnitt haben wir festgestellt, daß die Interpolation mit kubischen Splines, d.h. stückweise mit Polynomen 3. Grades, eine sehr glatte Kurve erzeugt. Erinnern wir uns, daß die intervallweise hermitesche Interpolation ebenso Polynome 3. Grades verwendet. Zusätzlich verläuft mindestens die 1. Ableitung an der Intervallgrenze stetig. Wenn nun die ersten Ableitungen $f\text{'}$_i an der Stützstellen $$_i, i=1,..n so bestimmt werden, daß die 2. Ableitungen dort auch stetig sind, kommen wir zu gleichen Polynomen 3. Grades wie bei der Spline-Interpolation.

Der Funktionsverlauf im Intervall $$ Element von [ _i , _i+1 ] ist vorgegeben durch:

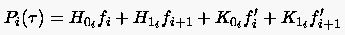(6.68)

Es wird verlangt, daß die Interpolation $f($) = P_i( ); Element von [ _i , _i+1 ] zweimal stetig differenzierbar ist, d.h.

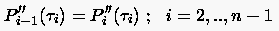(6.69)

oder

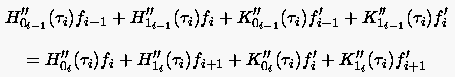(6.70)

Aus den Gleichungen (6.60) und (6.70) folgt nun die Bestimmungsgleichung für $f\text{'}$_i :

oder nach $f\text{'}$_i sortiert:

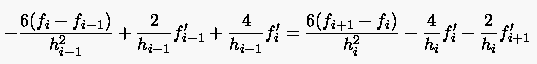
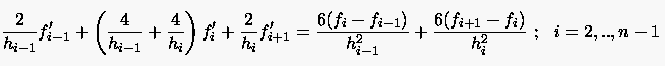(6.71)

Das Gleichungssystem wird entweder durch die Vorgabe der 1. Ableitungen $f\text{'}$₁ , f'_n oder durch die Vorgabe der 2. Ableitungen $f\text{'}\text{'}$₁ , f''_n an den Randpunkten mit der Beziehung:

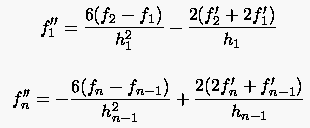(6.72)

geschlossen.