Die Erzeugung von Flächen im 3D-Raum

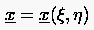
Die parametrische Darstellung von Flächen wird gegeben durch

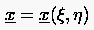(6.91)

Man kann z.B. eine Einheitskugel wie folgt darstellen:

Im allgemeinen Fall, insbesondere bei unregelmäßigen Geometrien, werden nur diskrete Punkte vorgegeben. Der Verlauf der Flächen im Raum muß daher interpoliert werden. Hier wird eine einfache Methode vorgestellt, die die Flächen zellenweise hermitesch interpoliert.

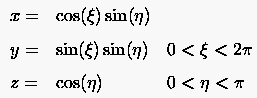
Seien die diskreten Punkte $x$_ij = x (_i , _j ) ( i = 1,..,I; j = 1,..,J ) vorgegeben, dann wird der Verlauf der Fläche in der Zelle $ij\; ($_i < < _i+1 ; _j < < _j+1 ) wie folgt interpoliert:

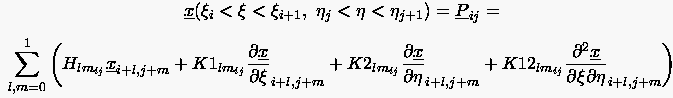(6.92)

mit

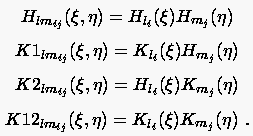(6.93)

Die zweimal stetige Differenzierbarkeit wird dadurch erreicht, daß man die Ableitungen des Ortsvektors

nach folgender Prozedur bestimmt:

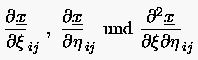
1. Schritt : Für 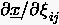$j\; (\; j\; =\; 1\; ,\; ..\; ,\; J\; )$ wird nach den Gleichungen (6.80)-(6.81) bestimmt. Dabei setzen wir den Kurvenparameter $$ anstelle von $$ ein.

2. Schritt : Für 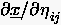$i\; (\; i\; =\; 1\; ,\; ..\; ,\; I\; )$ wird nach den Gleichungen (6.80)-(6.81) bestimmt. Dabei setzen wir den Kurvenparameter $$ anstelle von $$ ein.

3. Schritt : Für 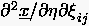$j\; (\; j\; =\; 1$ und $J\; )$ wird nach den Gleichungen (6.80)-(6.81) bestimmt. Hier wird nicht nur der Kurvenparameter $$ durch 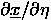ersetzt, sondern auch $x$ durch $x$ und $x\; \text{'}$ durch 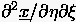. Dieser Schritt dient zur Erzeugung von Randwerten des nächsten Schritts und wird nur bei Bedarf einbezogen.

4. Schritt : Für $i\; (\; i\; =\; 1,\; ..\; I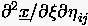\; )$ wird nach den Gleichungen (6.80)-(6.81) bestimmt. Hier wird der Kurvenparameter $$ durch $$ , $x$ durch 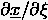und $x\; \text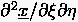{'}$ durch ersetzt.

Die obige Prozedur mag auf den ersten Blick kompliziert erscheinen. Sie ist aber im Grunde nur eine wiederholte Anwendung der im Abschnitt 6.5.4 beschriebenen alternativen Methode bezüglich beider Kurvenparameter.

Es ist festzustellen (ohne Beweis), daß die so interpolierte Fläche auf allen Zellengrenzen (nicht nur an den vorgegebenen Stützpunkten) zweimal stetig differenzierbar ist. Damit ist die Anforderung der zweimal stetigen Differenzierbarkeit in jedem Punkt der Fläche sichergestellt.

Die selben Flächen können natürlich auch durch klassische Spline-Interpolation erzeugt werden, indem man folgenden kubischen Polynomansatz für jede Zelle macht:

Die Berechnung der Koeffizienten $a$lm_ij erfolgt ebenso aus der Bedingung der zweifach stetigen Differenzierbarkeit. Außer dem unübersichtlichen Bestimmungsvorgang der Koeffizienten ist ein schwerwiegender Nachteil dieser Methode der 4-fach größere Speicherbedarf gegenüber der zellenweisen Hermiteschen Interpolation.

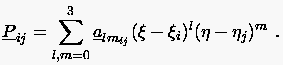
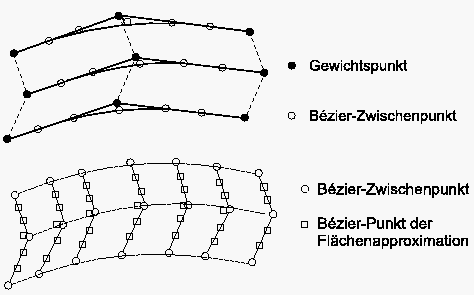
Bézier-Spline-Approximation von Flächen

Die kubische 2D-Bézier-Spline-Approximation stützt sich auf 16 Beźier-Punkte $B$lm_ij (l, m = 0,1,2,3) pro Zelle $ij\; ($_i < < _i+1 , _j < < _j+1 ) :

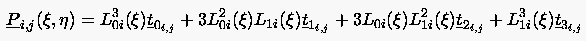(6.94)

mit (m = 0 , 1 , 2 , 3)

Die gesamte Fläche wird dann zellenweise zusammengestellt:

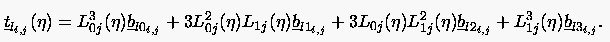
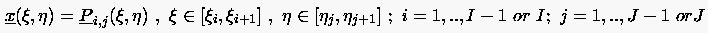(6.95)

Bei gegebenen Gewichtspunkten $V$_ij ( i = 1,..,I; j=1,..,J) werden die Bézierpunkte ohne nähere Beweisführung (das gleiche Prinzip wie im 1D-Fall) wie folgt berechnet:

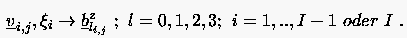
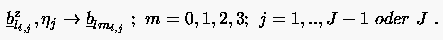
1. Schritt: Bestimmung der Bézier-Zwischenpunkte wie im Fall der 1D-Bézier-Approximation in i- bzw. $$-Richtung für alle Linien $$= _j ( j = 1,..., J ; jeweils einzeln betrachtet):

2. Schritt: Die Zwischenpunkte $bz$l_i,j werden als Gewichtspunkte der 1D-Bézier-Approximation in j- bzw. $$-Richtung für alle $l$_i-Linien ( l = 0,1,2,3; i=1,..,I-1 oder I; jeweils einzeln betrachtet) eingesetzt. Die erzeugten Bézier-Punkte der 1D-Approximation sind gleichzeitig die gesuchten 2D-Bézier-Punkte:

Das folgende Bild verdeutlicht den Bestimmungsprozeß:

Abbildung 64: Bestimmungsschritte der Bézier-Punkte der 2D-Approximation.