Adaptionstechniken

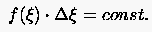
Grundsätzlich lassen sich die Adaptionstechniken in zwei verschiedene Klassen einteilen: Die eine enthält diejenigen Techniken, bei denen sich die Anzahl der Gitterpunkte und die Struktur ändert, die andere solche, wo dies nicht der Fall ist.

Bei der ersten Gruppe werden in Bereichen, an denen das Gitter verfeinert werden soll, einfach zusätzliche Zellen erzeugt. Die Erzeugung eines auf diese Art adaptierten Gitters ist nicht schwer, allerdings muß der Strömungslöser in der Lage sein, unstrukturierte Gitter zu verarbeiten, auch wenn das Ausgangsgitter strukturiert ist.

Techniken der zweiten Gruppe behalten die Struktur des Gitters und die Anzahl der Gitterpunkte bei. Die für eine Verdichtung erforderlichen zusätzlichen Zellen werden an Stellen, an denen kleine Gradienten der Strömungslösung vorliegen, 'abgezweigt'. Diese Methode soll nun näher beschrieben werden.

Eine einfache räumliche Diskretisierung von (6.144) ergibt:

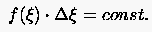(6.145)

mit $$ als Punkteabstand und $f($) als Gradient der Dichte zwischen zwei Punkten. (6.145) würde bei einem Nullgradient zwischen zwei Punkten einen unendlichen Punkteabstand erzwingen, was natürlich für ein Rechengitter nicht sinnvoll ist. Daher wird eine andere 'Fehlerfunktion' eingeführt, die (vom Benutzer einzugebende) Minimal- und Maximalabstände zwischen zwei Punkten berücksichtigt.

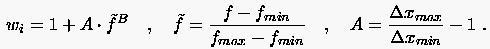(6.146)

Die Konstante B muß nun so bestimmt werden, daß der eingestellte Minimalabstand $$x_min dem Minimalabstand $MIN($x_i) entspricht. (6.145) ist die Euler-Lagrange-Gleichung für das Minimum von

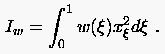(6.147)

Das Minimum von (6.147) entspricht der Minimalenergie eines Systems aus in Reihe geschalteten Federn mit den Federkonstanten $w($). Die Energie eines solchen Systems wird minimal, wenn die Produkte aus Abstand und entsprechender Federkonstanten gleich dem Produkt aus Gesamtlänge L und Ersatzfederkonstanten $w$_ers des Systems sind:

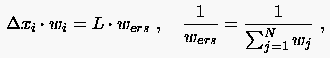(6.148)

$$ Punkteabstände

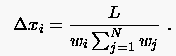(6.149)

Die Konstante B wird aus den Gleichungen (6.146) und (6.149) mit einer Newton-Iteration bestimmt:

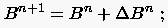(6.150)

mit hochgestelltem Index 'n' als aktuelle Iterationsebene. $$B ergibt sich zu:

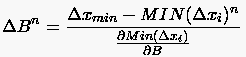(6.151)

Der Nenner in (6.151) läßt sich folgendermaßen angeben:

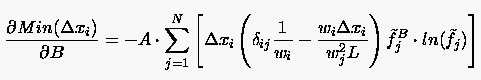(6.152)

Der beschriebene Algorithmus verhält sich so, als ob man zwischen die Zellwände Federn mit Federkonstanten nach (6.146) einbaut, was eine recht anschauliche Analogie ist.