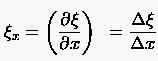
Bei der Transformation der partiellen Ableitung traten im vorangegangenen Abschnitt Faktoren der Art usw. auf, die wir Metrikkomponenten der Transformation nannten. Ihre geometrische Deutung ist naheliegend, sofern man näherungsweise
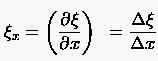
Tatsächlich läßt sich z.B. die Größe eines Flächenelements des Rechengebiets durch die Metrikkomponenten mit derjenigen des dazugehörigen Elements im Integrationsgebiet vergleichen. Von
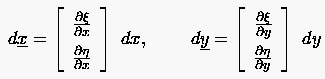 |
(6.17) |
folgt
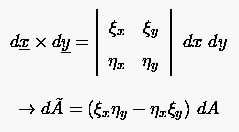 |
(6.19) |
oder aber für den Fall der inversen Abbildung
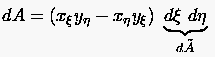
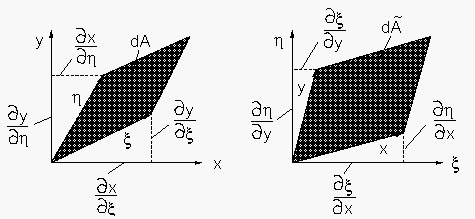 |
| (6.20) |
deren unabhängige Variablen lauten. Betrachtet man z.B. die -Komponente eines ebenen Geschwindigkeitsfeldes, so erhält man wegen
mit Hilfe des totalen Differentials
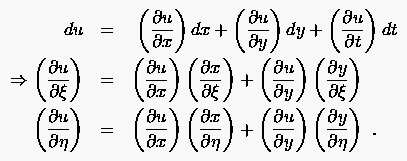 |
(6.22) |
Die Gleichungen (6.22) stellen ein gekoppeltes System von zwei Gleichungen für die beiden unbekannten partiellen Ableitungen und dar. Die Auflösung dieses Systems unter Verwendung der Cramer'schen Regel ergibt:
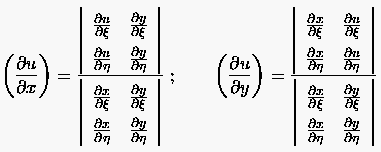 |
(6.23) |
Die Nennerdeterminante der Beziehung (6.23) nennt man Determinante der Jakobimatrix
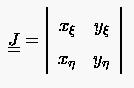 |
(6.24) |
mit
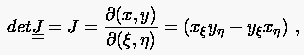 |
(6.25) |
so daß wir alternativ zu (6.23) auch
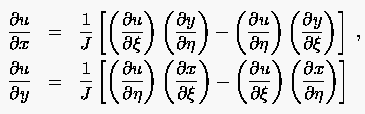 |
(6.26) |
verwenden können. Die Ausdrücke (6.26) geben Aufschluß über den Wert der
partiellen Ableitungen nach den freien Parametern des kartesischen
Systems in Abhängigkeit der partiellen Ableitungen in der transformierten Ebene
und inverser Metrikkomponenten 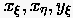 etc.
Der Fall
entzieht sich unserer Kenntnis. Es handelt sich dabei um eine
nicht eindeutig umkehrbare Abbildung ,
für die keine Rücktransformation der Ergebnisse ins Ursprungssystem möglich ist.
Schließt man derartig pathologische Fälle einmal aus, so läßt sich leicht zeigen,
auf welche Weise man die Metrikkomponenten aus einer gegebenen inversen Abbildung
gewinnt.
etc.
Der Fall
entzieht sich unserer Kenntnis. Es handelt sich dabei um eine
nicht eindeutig umkehrbare Abbildung ,
für die keine Rücktransformation der Ergebnisse ins Ursprungssystem möglich ist.
Schließt man derartig pathologische Fälle einmal aus, so läßt sich leicht zeigen,
auf welche Weise man die Metrikkomponenten aus einer gegebenen inversen Abbildung
gewinnt.
Die Abbildungen
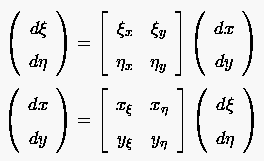
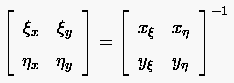
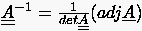 beschrieben, weshalb man
beschrieben, weshalb man
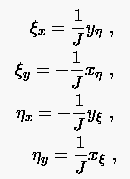 |
(6.30) |
findet.
Die Bogenlänge eines differentiellen Linienelementes der Ausgangskonfiguration wird durch die Beziehung
bzw. mit sowie
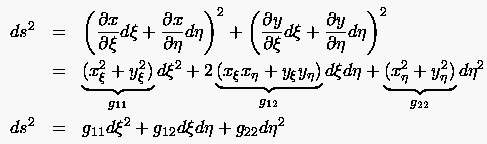 |
(6.32) |
beschrieben. Die darin auftretenden Metrikkoeffizienten
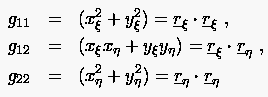 |
(6.33) |
nennt man auch die drei Gauß'schen Fundamentalgrößen erster
Ordnung. Diese lassen sich zu einer Matrix 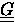 zusammenfügen
zusammenfügen
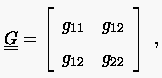 |
(6.34) |
deren Determinante durch
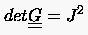 |
(6.35) |
festgelegt ist.
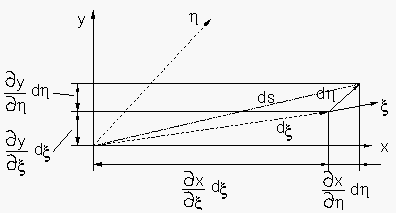 |
Metrikterme wie Gauß'sche Fundamentalgrößen dienen insbesondere zur Beschreibung der Gestalt des körperangepaßten Gitters in kartesischen Bezugssystem. Als erstes wollen wir in diesem Zusammenhang herausfinden, welcher Bedingung die Metrik im Falle orthogonaler Scharlinien genügen muß. Der örtliche Verlauf einer Parameterlinie im System wird durch den kartesischen Gradienen vektorwertig beschrieben. Die Orthogonalitätsrelation lautet somit
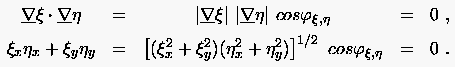 |
(6.36) |
Unter Berücksichtigung von (6.30) erhalten wir eine äquivalente Formulierung auf der Basis inverser Metrikkomponenten,
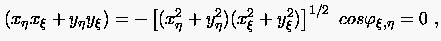 |
(6.37) |
aus der man die (lokale) Orthogonalitätsbedingung 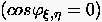
| (6.38) |
gewinnt. Häufig wünscht man sich einen glatten Verlauf der Parameterlinien im kartesischen System. Die Parameterwerte dürfen sich dann beim Fortschreiten in bzw. -Richtung nur geringfügig ändern. Ein geeigneter skalarer Richtwert ist durch die zu minimierende Beziehung (6.39) gegeben
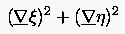 |
(6.39) |
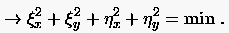 |
(6.40) |
Die Verwendung inverser Metrikkomponenten führt alternativ zu (6.40) auf
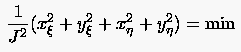 |
(6.41) |
bzw.
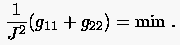 |
(6.42) |
Einheitliche Maschen- (bzw. Volumenzellen-) weiten enthält man aus
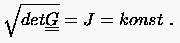 |
(6.43) |
Hierdurch wird eine gleichmäßige Genauigkeit im Feld gewährleitet.