Eindimensionale Wärmeleitung

Zunächst wird als Beispiel die Wärmeleitungsgleichung betrachtet:

(4.1)

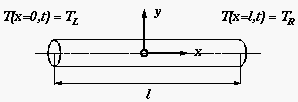
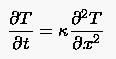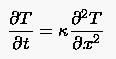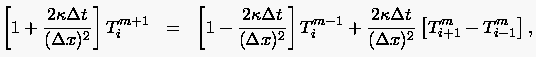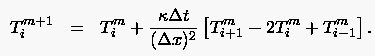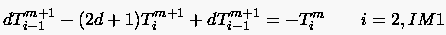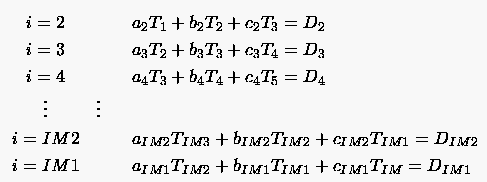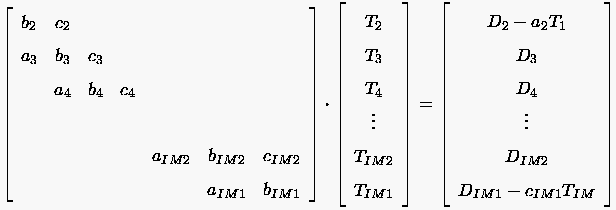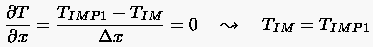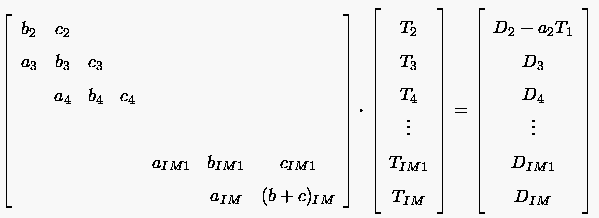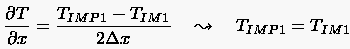Wir betrachten einen idealisierten Stab mit Wärmeübergang an seinen beiden Enden.

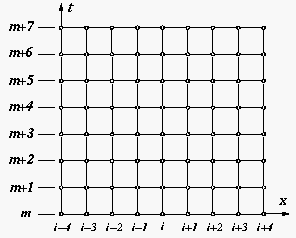
• Die expliziten Verfahren DF und FTCS erlauben die diskrete Berechnung der unbekannten Temperaturverteilung an den Gitterpunkten $T$_i^m durch eine entsprechende ''marching procedure''.

  DF: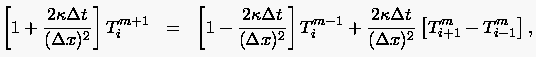

  FTCS: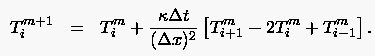

• Die impliziten Verfahren BTCS und CN führen auf algebraische Gleichungssysteme für die Temperaturverteilung $T$_i^m+1, i=1, IM. Für alle inneren Punkte lauten die algebraischen Gleichungen:

  BTCS: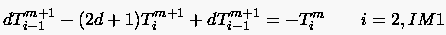

• Für konstante Diffusionszahl $d\; =$t / (x)² läßt sich das Gleichungssystem allgemein schreiben als

  $a$_i T_i-1 + b_i T_i + c_i T_i+1 = D_i

  Die Anwendung auf alle inneren Punkte zum Zeitpunkt $t$^m+1 ergibt:

  

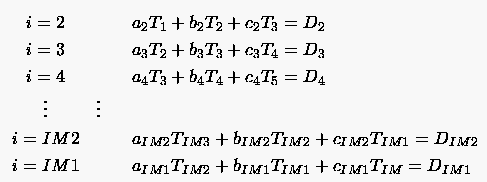
• Für Dirichlet-Randbedingungen sind die Randwerte $T$₁=T_L und $T$_IM=T_R bekannt, so daß umgeschrieben werden kann:

  $b$₂ T₂ + c₂ T₃ = D₂ - a₂ T₁

  $a$_IM1 T_IM2 + b_IM1 T_IM1 = D_IM1 - c_IM1 T_IM

• In Matrixschreibweise erhält man:

  

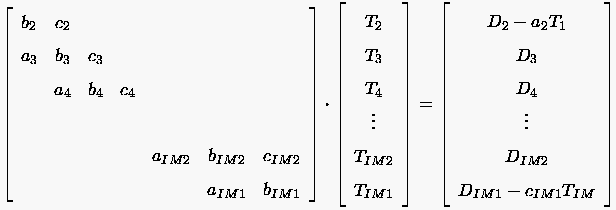
• Auch andere Randbedingungen ändern die tridiagonale Form der Koeffizientenmatrix nicht.

  Der Einbau einer Neumann-Randbedingung $$T/x=0 bei $i=IM$ ergibt

  

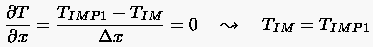
• Die algebraische Gleichung für $i=IM$ lautet

  $a$_IM T_IM1 + b_IM T_IM + c_IM T_IMP1 = D_IM

  $a$_IM T_IM1 + ( b_IM + c_IM ) T_IM = D_IM

  und die dazugehörige Matrixschreibweise

  

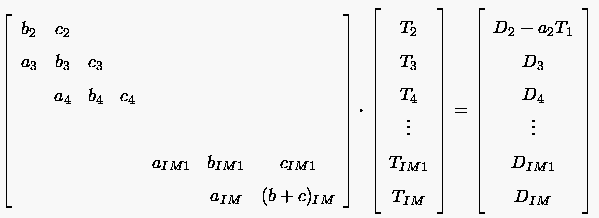
• Wird für die Neumann-Randbedingung eine Approximation $O($x²) verwendet,

  

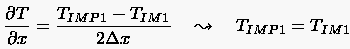
  dann lautet die angepaßte Gleichung $i=IM$

  $a$_IM T_IM1 + b_IM T_IM + c_IM T_IM1 = D_IM
  
  (a_IM+ c_IM) T_IM1 + b_IM T_IM = D_IM

• Die Lösung des Gleichungssystems kann iterativ (Jacobi, Gauss-Seidel) oder direkt (Elimination nach Gauss, LU-Zerlegung) erfolgen (siehe hierzu Kapitel 5).